Conjetura de Mertens — En matemáticas, la conjetura de Mertens fue una conjetura sobre el comportamiento de la función de Mertens cuando su argumento se incrementaba. Conjeturada como cierta por Franz Mertens en 1897, fue probado que era falsa en 1985. La conjetura de… … Wikipedia Español
Función de Mertens — En teoría de números, la función de Mertens se define como: donde μ(k) es la función de Möbius. Dado que la función de Möbius contempla solo las imágenes { 1,0,1} resulta obvio que la función de Mertens apenas varía en su recorrido y que no… … Wikipedia Español
Número primo — Un número primo es un número natural mayor que 1, que tiene únicamente dos divisores distintos: él mismo y el 1. Se contraponen así a los números compuestos, que son aquellos que tienen algún divisor natural aparte de sí mismos y del 1. El número … Wikipedia Español
Función de Möbius — La función de Möbius μ(n), nombrada así en honor a August Ferdinand Möbius, es una función multiplicativa estudiada en teoría de números y en combinatoria. Contenido 1 Definición 2 Propiedades y aplicaciones 2.1 Teoría de números … Wikipedia Español
Diecinueve — Este artículo trata sobre el número 19, para el año véase año 19 19 Cardinal Diecinueve Ordinal Decimonoveno, a Factorización 19 (número primo) … Wikipedia Español
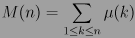 donde µ(k) es la función de Möbius, entonces la conjetura de Mertens postula que:
donde µ(k) es la función de Möbius, entonces la conjetura de Mertens postula que:
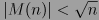 En 1885, Stieltjes afirmó haber demostrado este resultado, pero no publicó una demostración, probablemente porque descubrió que tenía un error.
En 1885, Stieltjes afirmó haber demostrado este resultado, pero no publicó una demostración, probablemente porque descubrió que tenía un error.